システムズリサーチコンサルタント　吉田繁治

データサイエンスとして、目指すべき方向と方法の2回目です。今回は「推計の統計学」について示します。これが小売業のデータサイエンスの基礎になるものです。といっても推計の統計学が何かを説明できる人は大学の数学科を出た人だけでしょう。

本稿では、具体例を中学の数学のレベルで示して、解説します。数学は純粋論理なので、基礎から示すと理解が進みます。

まず確認すべきことは、小売業の数値管理は、「商品へのアクションと対策のために行う」ことです。商品政策の結果である出力帳票の売上金額や数量を見るだけでは、結果観察（モニター）でしかない。

前年比の売上げが良かった、あるいは多くの場合、悪かったとなるだけであり、経営的には（成果責任を負う仕事としては）意味がない。会計的な実績データは、過去の経営の結果を株主に報告するものでしかないのです。

来月や来週（未来）に向かって仕事をする商品部や店長会議では、4週売上げや客数を観察し、売上げの予想に基づいて、対策のアクションが検討され、決定されなければ意味がない。

会社の会議は売上げ、利益、生産性の、過去の原因の究明と、未来の対策の、PDCA（目標→実行→管理→対策）の立案のためものです。

「売上げが良くない」と評価される場合、その原因を推計し、原因対策を立てて、実行することが仕事の義務（＝職務）です。PDCAが示す内容がこれです。

平均値の種類は多い

コンピュータ数表のあらゆるデータは、一定期間の「合計または平均」です。

小売業では、売上げの13週、4週、1週が時間の基準です。スーパーマーケット（SM）の生鮮は、毎日発注するので、日量（金額と数量）です。

顧客の買物行動は曜日の生活習慣があるので、会計から来た古い方法である月次集計は、データサイエンスには適切ではない。売上データの利用で最も、実務的な効果を挙げるのは、来週または明日の売上数予想による発注数の決定です。これはいろいろな平均値を使って、行います。

実はここが、AI（人工知能）にもつながる小売業のデータの数理（データサイエンス）の最も基礎の一例になるものです。売上げには、増加または減少の傾向があります。傾向がなければ、合計をデータ数で割る単純平均、{（D1＋D2＋D3…Dn）÷n}の売れ数を予測としていい。

しかし売上げのように、上昇、下落の傾向を持つ場合は、過去のデータの単純平均では予想の誤差が大きくなります。図表の、単純化した数表を見てください。統計関数を多数持つExcel上に作ったものです。

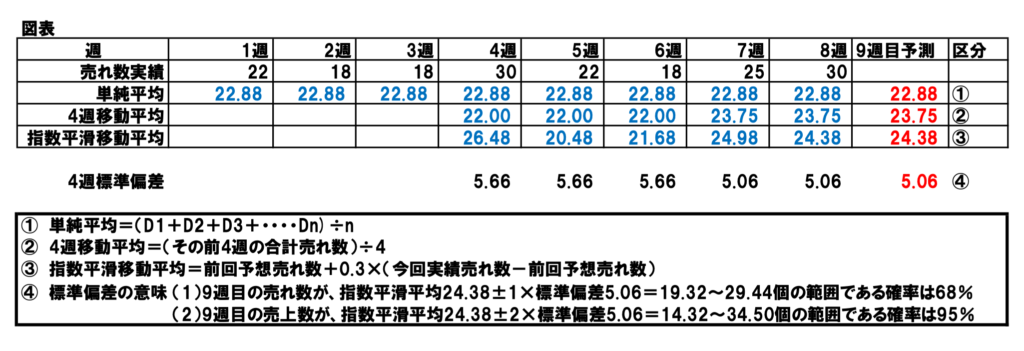
8週間の、ある品目の1店舗の売れ数が、22、18、18、30、22、18、25、30と変化しています。次回の発注のため、9週目の売れ数を予測するものです。この生データだけでは、9週の予想は困難です。

予想では平均値を使いますが、平均には統計学的に、たくさんの計算方法があるのです。本稿では、4つを示します。

データサイエンスとは、平均の統計学の利用を行うものです。数字を合計して平均するのは、一個一個では意味が薄いデータを、1つの数字で代表させるためです。つまり平均は、多くのデータの代表です。代表とは「代わりに表すもの」です。

①「単純平均」では、8週の1週売れ数は22.38個になります。この説明の必要はないでしょう。小学校で習う普通の平均です。時間軸での傾向がないとき、8個の売上データを22.38個で代表させるのです。

ランダムに計る身長では、次に計る人に傾向がない。このため単純平均でいい。サイコロを振ったときの平均も、目が出る確率は6分の1ですから、平均は{（1+2+3+4+5+6）÷6=3.5｝としていい。しかし、傾向を持つ売上げには、単純平均は不適当でしょう。

②は、「4週移動平均」です。平均を取る期間を4週として、1週ずつずらして取った平均が4週移動平均です。

移動平均にすると、単純平均では見えない、売れ数の傾向が、なだらかになって見えてきます。ここが重要な点です。「移動平均は、ばらつきを吸収してデータの傾向を示す」。

事例の図表の4週移動平均で見ると、4週目が22.00、5週目、6週目も22.00個です。7週目の25個への売れ数の増加を反映し、7週目は22.75個に増えています。

8週目は売れ数30個のへの増加を反映し、23.75個に増えています。

4週移動平均の売れ数予測では、9週目は、この23.75個です。

発注には売れ数予測データを使います（図表の4週移動平均②）。

③は、移動平均の中で、多少高度な「指数平滑移動平均」です。単純な移動平均では、データの重みが全部同じです。

一方、指数平滑移動平均は、加重移動平均です。近いデータの重み（比重）を、平滑指数のパラメータで、上げていくものです。現在に近いデータが、明日のデータを左右する度合いが大きいと見て、数学者が作ったものが、この加重移動平均です。

図表の事例では、加重と決める平滑指数で最もよく使われる0.3を平滑指数にしています。

計算式は、{前回予測値＋平滑指数0.3×（今回の売れ数実績‐前回予測値）}です。

この式を見れば分かるように、前回予測値とその売れ数実績との差異に0.3をかけて、修正していくものです。これが指数平滑法、つまり、加重移動平均です。

株価の短期予想では、MACD（Moving Average Convergence Divergence）として、売買のタイミングを判断するテクニカル分析で、最もよく使われています。

ほぼ100％のトレーダーが、20日や50日の移動平均線とMACDを組み合わせて使い、金利や企業利益のニュース（イベント）を加味して、売買の時期を判断しています。株価ではいつ買うか、いつ売るかで利益が決まるからです。みな利益を目的にして株を売買しています。

株価には、品目の売れ数のように上昇と下降の短期傾向がありますが、それを数学的に捉える適正な方法が指数平滑予測です。

図表①の事例の③の、9週目売れ数予測の24.38個は、4週移動平均の23.75個より0.63個大きい。これは、7週実績の25個、8週実績の30個への増加を反映したものです。

指数平滑法は加重移動平均ですから近いデータの重みが大きな平均です。売れ数の変化への追随性が、移動平均より強くなります。なお、指数平滑法を含む統計関数（数式＝ｆ（ｘ））は、Excelには十分すぎるくらい入っています。

関数の活用で試されるのは、あなたの、統計学への知識のレベルです。小売業のデータサイエンスとは、売れ数の統計学です。筆者は、あからさまな真実を述べています。

次は④の標準偏差です。これが、およそ95％の人の理解の難所になっています。

統計学の母が、標準偏差です。テストの成績の偏差値でおなじみのものですが、その意味を説明できる人は極めて少ないのです。

偏差値は、テストの成績での、個人の分布の位置を示す標準偏差ですが、50点を真ん中にするため、50を加えています。数式は以下です。

偏差値=（あなたの得点-平均点）÷全員の得点の標準偏差×10+50。

この標準偏差が、全員の得点の分布を示します。

標準偏差の計算式は、「（各データ-平均=平均との差異）を2乗して合計し、データの個数で割って、平方根を取ったもの」です。

標準偏差は、平均からの「平均的な差異」を確率で示すのものです。

標準偏差では、過去の事実データ（ここでは品目の売れ数）も、確率的に変動した結果であると見ます。

近い将来の売上げは、同じように確率変動する性質が強いので、過去の事実データで計算した標準偏差を未来に適用して、売上げを予測するのです。

図表の④の8週目標準偏差の数値は5.06個です。この5.06は何を意味しているのか。まだない9週目以降の売れ数が、68％含まれる範囲です。

具体的には、「指数平滑の9週予測値24.38個±標準偏差5.06＝19.32個～29.44個≒19個～29個」の範囲に、まだない9週売れ数が68％含まれると推計できるということです（1シグマ:1σという）。

この標準偏差の2倍を取って、「指数平滑の9週予測値24.38個±2×標準偏差5.06＝14.32個～34.5個≒14個～35個」とすると、9週売上げの確率は95％に上がります（2シグマ:2σという）。

標準偏差は、生産管理での品質検査に使われます。生産品のサンプルの品質を検査し、何%の確率で、不良品が出ているかを調べる近代生産の方法です。

例えば、標準偏差の6倍（シックスシグマ:6σ）を取ると、不良品率は100万分の1になります。これがソニーの部品生産で採用されているものです。

一般に、発注のときは事例の品目の、店舗展示欠品を2.5％にする2シグマの標準偏差を加えた、35個を使います。「35個-発注時の有効在庫残数7個＝28個」を発注したときの、9週目の欠品確率は2.5％（40週に1回）です。

以上から、定期発注法の発注公式を導くことができるのです。

「9週目に向けた最適発注数＝指数平滑予測数24.38個＋安全在庫10.12個－発注時の在庫残数7個＝27.5個≒28個」

今回は、28個発注すれば、職務責任が果たせます。

この計算は、コンピュータに計算式を入れておけば、自動計算できることが分かるでしょう。

データサイエンスは、計算式をコンピュータに入れた自動計算です。計算式を作らないとプログラムにできません。

AIの方法は多変量解析

AIでは、売れ数の変化が起こる天候や気温などの、データセット（過去の実績データを字時系列で並べたもの）を深層学習させて加え、最小二乗法（傾向を持つ傾き）の計算で変数を加えた、多変量解析の方程式になります。9週目の、天候と平均気温の温度の予想も必要です。

天候による売れ数の変化が大きな商品発注の、数式の原型を示します。

「9週目に向けたAI最適発注数＝指数平滑予測数24.38±α×天候変動±β×気温変動・・・＋安全在庫10.12個-発注時の在庫残数7個」。

天候や温度の要素を加えなかった28個の発注に対して、数個の多さ、または少なさの違いが出るでしょう。

ただし、AIで天候変動を加えても、毎週発注の場合は、欠品を起こさない限り、次回発注から在庫残が引かれるので、AIによって在庫効率が上がり、売上げが増えるとはいえません。

しかし、例えば、海外工場での衣料の開発で、3カ月分のロットを発注予約するときには、衣料の売上げを左右することが多い次のシーズンの天候と気温の予測の要素を加えることは意味があります。

1回で10万枚（≒1枚の仕入れ原価が1000円なら生産原価は10万枚で1億円）の生産予約を、海外工場に行う職務責任のバイヤーなら、冷夏や厳冬の要素を入れることは、経験的に行っているはずです。

下手をすれば数千万円の機会損失や過剰在庫が出るからです。

ヘッジファンドトレーダーに似た、予想イベントの数値管理（データサイエンス）が必要です。金利や企業の利益の予想と、織り込みです。

それでは、指数平滑の売れ数予測に、売上げのばらつきの幅を示す標準偏差の2倍を入れないで発注した場合は、9週目の結果はどうなるか。

欠品が50％の確率で起こります。2回に1回の発注で、欠品が起こって、売上げの機会損失が発生します。この金額は大きなものになるでしょう。

機会損失の発生を2.5％（40回に1回）に防止するため、その週は過剰在庫になることもある安全在庫を加えるのです。もちろんこれは、消費期限のない商品のときの発注です。

その点、SMやコンビニの生鮮のように消費期限が1日から数日と少ない商品では、発注の頻度が毎日になります。

安全在庫は、日量の平均売れ数の8％くらいが部門の営業利益に対して最適という結果が、Excelの乱数を使った当方のシミュレーションで出ています。

売れ数の標準偏差（数学的変動幅）の解析を使わず、バイヤーが「勘（カン）」で、安全在庫を加えているケースが多いと推測します。

指数平滑移動平均を含む平均値だけの発注では、50％の確率で次週の陳列在庫欠品が生じるからです。2回に1回欠品していれば、バイヤーの職務責任は果たせません。

しかしこのカンによる安全在庫では、時期よって売れ数の数値の大きさ、小ささ、そしてバイヤー個人によってもばらつきが大きくなります。

ここで示した標準偏差を使うデータサイエンスでは、適正発注数のばらつきをなくし、標準化する効果があるのです。数値管理は、作業の標準化によって果たされます。

データサイエンスでは、誰でも、いつでも、最適数の発注ができるようになり、店舗の売上増収と営業利益の双方において効果を生みます。

なお、一般的な、定期発注の、コンピュータに組み込む公式は以下です。ここまで読んでいれば、理解は容易でしょう。

定期発注数＝（発注サイクル日数+入荷リードタイム）×日量の売上予測数+2×日量売上げの標準偏差×√（発注サイクル日数+入荷リードタイム）-発注時点有効在庫数。

集配センター（DC）の在庫が発注点に減ったとき、コストが最適になるロット数（定量）の発注を、工場に行うときの公式は以下です。プライベートブランド商品の海外生産で使うことが多い。

発注点在庫数＝DCへの入荷リードタイム日数×店舗の1日平均売れ数+2×1日売れ数の標準偏差×√（入荷リードタイム日数+発注間隔日数）

Excelでは、期間を指定したSTDEVの関数で自動計算されます。

データサイエンスの効果

発注公式を事例にして示したデータサイエンスで使う推計の統計学には、適正な在庫数と在庫運用の側面だけでなく、店舗の棚売上げと利益の面も最適化する性質を備えています。

店舗で使われる定期発注法を、数回繰り返すと、棚の在庫数は、売れ数に比例していきます。

1週間に10個売れる商品と3個しか売れない商品の、平均在庫数が3:1になって行くのです（売れ数比例在庫という）。

これは在庫回転数が一定値でそろっていくことを意味します。つまり売上げに対して、無駄な在庫と陳列スペースがなくなっていくのです。売れ数の多い品目の陳列在庫数は多くなり、売れ数が少ない品目の在庫数は少なくなっていくからです。

品目当たりの、在庫数の適正化の効果は、バイヤーの職務責任である、1坪当たりの売上げの増収と、営業利益の増加です。

本稿では、平均と標準偏差のデータサイエンスを使う予測発注（これが、適正な在庫管理です）を述べました。

数学の用語に慣れていない人は、繰り返し読むと、3回から5回くらいで分かります。

文系の人には、数学が不得意だった人も多いでしょう。今回書いた標準偏差の指数平滑法の理解がデータサイエンス基礎として必須です。

リテールトレンドでは、情報・サービスの関連サービスをご紹介しています。

詳しくはこちらより、ご確認ください。